因为有限元分析中要用到一些材料力学方面的知识,因为没学过塑性力学所以了解了一下相关知识,本文视作自己记录之用,以后还可以翻翻,省得再去找一堆资料了。
首先,材料力学中工程应力定义为:
$$ \alpha = \frac{F}{A_0} $$
式中$A_{0}$为初始横截面面积,$F$为拉伸试验的作用力。
工程应变的定义公式为:
$$ \varepsilon = \frac{l-l_0}{l_0}= \frac{\Delta l}{l_0} $$
式中$l_0$为初始长度,$l$ 为拉伸后长度。
根据拉伸试验可以得到以下大致的关系图:(请原谅我盗个图)
╭( ′• o •′ )╭☞警察叔叔!就是这个人(。•ˇ‸ˇ•。)
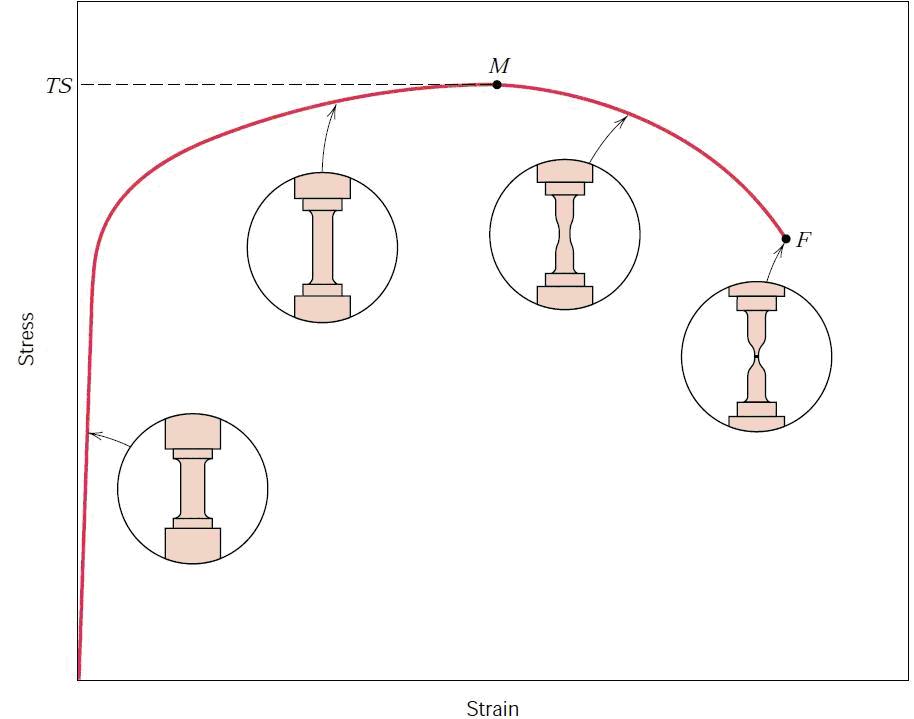
在实际的拉伸过程中材料会发生颈缩现象,横截面积在变化,所以工程应力应变并不能准确反映材料在拉升过程中的变化。根据工程应力的定义我们可以得出真实应力的定义公式:
$$ \sigma_T = \frac{F}{A_T} $$
式中 $A_T$ 表示在拉伸过程中的实际横截面积。
对于大多数金属来说,根据不可压缩性,可以得到以下公式:
$$ l_0A_0=lA_T $$
$$ \therefore A_T=\frac{l_0A_0}{l} $$
代入真实应力定义公式有:
$$ \sigma_T = \frac{Fl}{A_0l_0}= \sigma \frac{l}{l_0} $$
根据工程应变定义可以得到:
$$ \frac{l}{l_0}=1+ \varepsilon $$
$$ \therefore \sigma_T=\sigma(1+\varepsilon) $$
这个公式就是真实应力与工程应力应变的关系
对于真实应变,首先我们可以根据定义得出单位时间内的应变为:
$$ \Delta\varepsilon = \frac{\Delta l}{l} $$
式中$l$为拉伸过程中的长度。上面这个式子可以写成:
$$ \mathrm{d}\varepsilon_T = \frac{\mathrm{d}l}{l} $$
有木有感觉到还是熟悉的味道,还是熟悉的配方,来个积分就变成了以下这个模样:
$$ \int{\mathrm{d}\varepsilon_T} = \int_{l_0}^{l} \frac{\mathrm{d}l}{l} $$
然后就有:
$$ \varepsilon_{T} = \int_{l_0}^{l} \frac{\mathrm{d}l}{l} = ln \frac{l}{l_0} $$
这个就是真实应变的计算公式。然后根据工程应变公式就可以得到真实应变与工程应变的关系式:
$$ \varepsilon_T = ln(1+ \varepsilon) $$
我们再看看工程应变和真实应变到底相差多少,这里要用到我一直很讨厌的泰勒级数展开(可惜不是斯威夫特):
$$ \varepsilon_T = ln(1+ \varepsilon)= \varepsilon - \frac{\varepsilon ^2}{2} + \frac{\varepsilon ^3}{3}- \frac{\varepsilon ^4}{4}+ \cdots $$
从这里可以看出当变形程度很小时(大致10%),$\varepsilon_T$和$\varepsilon$几乎相等。
经过上面的一堆吧啦吧啦和巴巴拉魔法后,只要记住两个关系公式就行了:
$$ \sigma_T=\sigma(1+\varepsilon) $$
$$ \varepsilon_T = ln(1+ \varepsilon) $$
来看个直观一点的曲线图吧:(咳咳,你懂的)
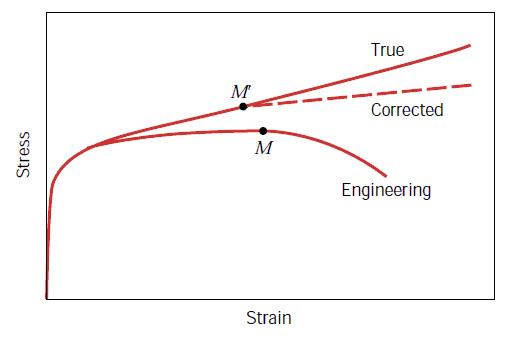
图中Corrected曲线是考虑到颈缩之后复杂的截面状况做的修正,其实我也不懂(@_@;),哇哈哈,以后再深究。

